Tugas 2 Sistem Pakar

-
Gambar
1.       Pakar  adalah orang yang mempunyai keahlian dalam bidang tertentu sedangkan kepakaran adalah pengetahuan yang dimiliki oleh seorang pakar melalui rangkaian penelitian. Informasi dan pengalaman.   2.       Perbedaan data, informasi dan pengetahuan : Data  adalah deskripsi dari sesuatu dan kejadian yang kita hadapi. Contohnya : a.        Kecelakaan di jalan. b.       Konstruksi jalan. c.        Naiknya harga bahan bakar.   Informasi  adalah data  yang diolah menjadi bentuk yang lebih berguna dan lebih berarti bagi yang menerimanya. Contohnya : a.        Kita mendapat surat pemberitahuan dari kampus. b.       Mendapat sms yang berisi penawaran paket kuota murah.   Pengetahuan  adalah  informasi  yang telah dikombin...
Posting Komentar

Tugas Kalkulus

-


Soal :
1)      y = x2 – 25
2)      y = -x2 + 7x – 12
3)      y = -x2 – 8x + 9
4)      y = -2x2 – 7x + 4
5)      y = -x2 +6x

JAWABAN

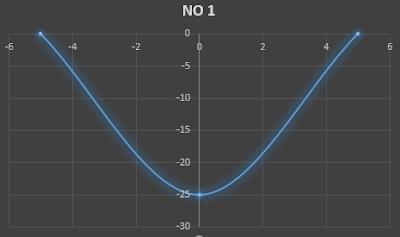
1.       y = x2 – 25

Titik potong sumbu –x ( y = 0)
y = x2  – 25
0 = x2 – 25

( x – 5 ) ( x + 5)
 x = 5    x= -5
koordinat titik potong sumbu –x (5,0) dan (-5,0)

Titik potong sumbu –y( x = 0 )
y = x2 – 25
y = 0 – 25
y = -25
koordinat titik potong sumbu –y ( 0, -25)

Koordinat titik puncak (xp,yp)
xp= -b/2a
xp= -0/2 . 1
xp= -0/2
xp= 0

yp= -b2-4ac / 4a
yp= -02 - 4.1.-25 /4.1
yp= -0 + 100 /4
yp= -25
koordinat titik puncak (xp,yp) = ( 0, -25 )






2.       y = –x2  + 7x – 12

Titik potong sumbu –x ( y = 0)
y = –x2  + 7x – 12
0 = -x2 + 7x -12
0 = x2 - 7x +12
( x – 4) ( x – 3 )
x = 4    x = 3
koordinat titik potong sumbu –x ( 4,0) dan  ( 3,0 )

Titik potong sumbu –y( x = 0 )
 y = -x2 + 7x -12
 y = -02 + 0 -12
 y = -12
koordinat titik potong sumbu –y ( 0,-12 )

Koordinat titik puncak (xp,yp)
xp= -b/2a
xp= -7/2.-1
xp= 7/2

yp= -b2-4ac / 4a
yp= -72-4.-1. -12/ 4.-1
yp= -49-48 / -4
yp= 97 / 4
koordinat titik puncak (xp,yp)  ( 7/2, 97/4 )



3.       y = –x2 – 8x + 9

Titik potong sumbu –x ( y = 0)
y = –x2 – 8x + 9
0 =-x2 - 8x +9
 x2 + 8x -9 = 0
( x + 9 ) ( x – 1 )
x = - 9     x = 1
koordinat titik potong sumbu –x ( - 9,0 ) dan  ( 1,0)

Titik potong sumbu –y( x = 0 )
Y =-x2 - 8x +9
0 =-02 - 0 +9
Y = 9
koordinat titik potong sumbu –y ( 0,9)

Koordinat titik puncak (xp,yp)
xp= -b/2a
xp= -(-8) /2.-1
xp= -4

yp= -b2-4ac / 4a
yp= -(-8)2-4.-1. 9/ 4.-1
yp= -64+36 / -4
yp= -100 / -4
yp= 25
koordinat titik puncak (xp,yp)  (-4, 25 )




4.       y= –2x2 – 7x + 4


Titik potong sumbu –x ( y = 0)
y = -2x2-7x + 4

0 = -2x2-7x + 4
 2x2+7x - 4 = 0
1/2 (2x + 8) ( 2 x – 1 )
( x + 4 )  ( 2 x – 1 )
x = -4      2x = 1
                x = 1/2
koordinat titik potong sumbu –x ( -4, 0) dan ( 1/2, 0 )

Titik potong sumbu –y( x = 0 )
y = -2x2-7x + 4
y = 0-0+ 4
y = 4
koordinat titik potong sumbu –y ( 0,4)


xp       = -(b/2a)
            = -(-7/2.-2)
            =-(-7/-4)
            = - 1,75

yp       = -(b2 – 4ac/4a)
            =- (72 – 4.-2.4/4.-2)
            = -(49 + 32/-8)
            = -(-10,125)
            = 10,125
koordinat titik puncak (xp,yp)  (-1,75; 10,125)





5.       y = –x2 + 6x

Titik potong sumbu –x ( y = 0)
y = -x2 + 6x
0 = -x2 + 6x
x2 - 6x =0
x ( x - 6 )
x = 0   x = 6
koordinat titik potong sumbu –x ( 0, 0) dan ( 6, 0 )

Titik potong sumbu –y( x = 0 )
y = -x2 + 6x
y = -02 + 0
y = 0
koordinat titik potong sumbu –y ( 0,0)
Langkah 3
Koordinat titik puncak (xp,yp)
xp= -b/2a
xp= -6/2.-1
xp= 3

yp= -b2-4ac / 4a
yp= -62-4.-1.0 / 4.-1
yp= -36-0 / -4
yp= 9
koordinat titik puncak (xp,yp) ( 3,9)





#UMMI
#KALKULUSINFORMATIKA
#HMIFUMMI
#UNIVERSITASUNGGUL
#SUKABUMI



Komentar

Posting Komentar

Postingan populer dari blog ini

Besaran, Satuan, Dimensi dan Persamaan di Dalam Listrik

-
Gambar
1 . Besaran dan Satuan Besaran diartikan sebagai sesuatu yang dapat diukur, serta memiliki nilai besaran (besar) dan satuan. Sementara, satuan digunakan sebagai pembanding dalam pengukuran. Satuan Internasional (SI) adalah satuan hasil konferensi para ilmuwan di Paris, yang membahas tentang berat dan ukuran. B erdasarkan satuannya,  besaran terdiri dari besaran pokok dan besaran turunan . 2. Besaran dan Satuan Listrik 3. Prefix/ Awalan Satuan SI Dalam kelistrikan terdapat beberapa besaran, dimana setiap besaran itu mempunyai simbol dan satuan yaitu : 1. Satuan Elektro Statis (SES) 2. Satuan Elektro Magnetis (SEM) 3. Satuan Praktis Satuan yang dipakai sekarang ini adalah satuan praktis, karena dua satuan yang lain terlalu rumit untuk dipakai. Berikut adalah besaran dan simbol beserta satuannya : Tegangan Listrik Tegangan listik yaitu perbedaan potensial listrik antara dua titik dalam rangkaian listrik, dan dinyatakan dalam satuan vo...
Baca selengkapnya

Komponen Elektonika

-
Gambar
 Pada Pengenalan komponen elektronika ini akan dibahas jenis-jenis komponen elektronika, fungsi komponen elektronika, beserta simbol yang digunakan pada komponen elektronika.             Komponen elektronika adalah alat berupa benda yang menjadi pendukung suatu rangkaian pada peralatan elektronika yang bekerja sesuai dengan fungsinya. Baik yang menempel langsung ke CCB, PCB, Veroboard dan Protoboard ataupun jenis papan rangkaian lainnya, ataupun yang tidak menempel langsung pada papan rangkaian seperti kabel. Secara umum, komponen elektronika dapat dibagi atas 2 macam berdasarkan fungsi kerjanya yaitu komponen elektronika pasif dan komponen elektronika aktif. •Komponen Pasif adalah komponen elektronika yang dapat beroperasi tanpa memerlukan arus atau tegangan listrik tambahan saat bekerja. Contoh komponen pasif yaitu resistor, kapasitor, induktor,  dan trafo atau tranformator. •Komponen Aktif adalah komponen ...
Baca selengkapnya